- 딥러닝
- SPP-Net
- image classification
- Weight initialization
- LeNet 구현
- deep learning
- Convolution 종류
- object detection
- overfeat
- Optimizer
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Today
- Total
목록전체 글 (56)
I'm Lim
 AdaGrad / AdaDelta / RMSprop
AdaGrad / AdaDelta / RMSprop
Paper Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016). 논문이 가지는 의미 다양한 optimization 기법을 통해 어떠한 이유로 optimization이 발전해왔는지에 대해 고찰해볼 수 있다. 또한, 어떤 optimization 기법을 사용해야 될지에 관한 직관을 키울 수 있다. 1. Adaptive Gradient (AdaGrad) AdaGrad Optimizer는 기존의 learning rate 파라미터를 가변적으로 조절함으로써 성능을 개선시키기위해서 고안되었다. 자세히 말하자면, 많이 업데이트되는 파라미터의 learning rate는..
 Momentum / Nesterov Accelerated Gradient
Momentum / Nesterov Accelerated Gradient
Paper Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016). 논문이 가지는 의미 다양한 optimization 기법을 통해 어떠한 이유로 optimization이 발전해왔는지에 대해 고찰해볼 수 있다. 또한, 어떤 optimization 기법을 사용해야 될지에 관한 직관을 키울 수 있다. 1. Momentum Gradient Descent 글에서도 설명했다시피 BGD, SGD, Mini-batch GD는 local minimum이나 saddle point를 잘 빠져나오지 못한다. 이는 다시말해 손실함수가 global minimum으로 도달하지 못해..
 Global Minima / Local Minima / Saddle Point
Global Minima / Local Minima / Saddle Point
Global Minimum loss function에서 loss 값이 가장 작은 지점. 이 지점에 도달하는 것이 딥러닝 학습의 최종 목표이다. Local Minimum Global Minimum이 아닌 극소점. 이것이 문제가 되는 이유는 딥러닝에서는 Gradient Descent를 이용하여 가중치 업데이트를 하는데 ($\theta = \theta - \eta * J(\theta)$; BGD) 극소점에서는 모든 가중치들의 기울기 값이 0이 되므로 더이상 가중치를 업데이트 시키지 못하기 때문이다. Saddle Point - Paper : Dauphin, Yann N., et al. "Identifying and attacking the saddle point problem in high-dimensional..
 Gradient Descent
Gradient Descent
Paper Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016). 논문이 가지는 의미 다양한 optimization 기법을 통해 어떠한 이유로 optimization이 발전해왔는지에 대해 고찰해볼 수 있다. 또한, 어떤 optimization 기법을 사용해야 될지에 관한 직관을 키울 수 있다. 1. Vanilla Gradient Descent (Batch Gradient Descent; BGD) 하이퍼 파라미터 - $\eta$ : learning rate로써 계산된 loss function의 gradient를 얼만큼 weight 업데이트시 반영할 것인가..
 Optimizer
Optimizer
Weight Optimization이란? 딥러닝 네트워크를 모델링 한 후, 이 모델에서 출력하는 예측값과 실제값과의 error를 이용해서 모델의 weight를 update 시키는 방법 Loss function 예측값과 실제값의 error를 정의하는 함수. 대표적인 예로 회귀문제에는 MSE Loss를 loss function가 있고, 분류문제에는 Cross Entorpy Loss가 있다. 위 그림은 MSE Loss를 시각화 시킨 것이다. 주목할만한 점은 x축이 w이고, y축이 J(w)라는 것이다. w는 weight를 의미하고, J(w)는 Loss function을 의미한다. 즉, J(w)는 w라는 가중치 행렬을 가진 모델의 예측값과 결과값의 차이다. 따라서, $J(w) = {\dfrac {1}{N}} \S..
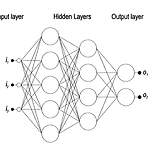 Multi Layer Perceptron
Multi Layer Perceptron
Paper Gardner, M. W., & Dorling, S. R. (1998). Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences. Atmospheric environment, 32(14-15), 2627-2636. 논문이 가지는 의미 인공지능망이 어떤 프로세스를 거쳐서 학습이 되는지 또 인공지능망을 적용한 예시 등을 보여줌으로써 기초적인 딥러닝의 학습방식을 이해할 수 있다. 논문의 내용 1. 딥러닝의 장점 1) 입력 데이터 분포에 대한 사전지식이 없어도 된다. 기존의 statistical model (e.g., Linear Regression, Logisti..
 Back Propagation
Back Propagation
Paper Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. nature, 323(6088), 533-536. 논문이 가지는 의미 퍼셉트론이 XOR문제를 해결하지 못하자 MLP가 등장하였고, 그에 따라 weight와 bias의 개수가 급등하였다. 이런 상황에서 weight update를 효율적으로 할 수 있는 방안이 필요했고, 그 중 하나가 Back-propagation 방식이다. 현재 딥러닝에서도 Back propagation을 이용하여 모델의 weight를 update시킨다는 점에서 중요한 논문이라 할 수 있다. 논문의 내용 1. Hidden layer..
 The Perceptron
The Perceptron
Paper Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review, 65(6), 386. 논문이 가지는 의미 최초의 Multi Layer Perceptron(MLP)에 대한 논문으로써 인공지능의 기원을 살펴볼 수 있다. 논문의 내용 1. 사람은 어떤 정보를 기억하는가? 1 ) One-to-one mapping : 어떤 정보를 고유의 코드화를 시켜서 저장한다는 것. 이 가설은 단순하여 임베딩이 쉽고, 직관적으로 이해하기 쉽다는 장점이 있다. 2 ) Central Nervous System (CNS) : 특정 정보를 임베..
