- object detection
- overfeat
- 딥러닝
- deep learning
- Convolution 종류
- Optimizer
- SPP-Net
- Weight initialization
- image classification
- LeNet 구현
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Today
- Total
I'm Lim
AdaGrad / AdaDelta / RMSprop 본문
Paper
Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016).
논문이 가지는 의미
다양한 optimization 기법을 통해 어떠한 이유로 optimization이 발전해왔는지에 대해 고찰해볼 수 있다. 또한, 어떤 optimization 기법을 사용해야 될지에 관한 직관을 키울 수 있다.
1. Adaptive Gradient (AdaGrad)
AdaGrad Optimizer는 기존의 learning rate 파라미터를 가변적으로 조절함으로써 성능을 개선시키기위해서 고안되었다.
자세히 말하자면, 많이 업데이트되는 파라미터의 learning rate는 줄이고, 적게 업데이트되는 파라미터의 leanring rate는 키우는 방식을 취한다. 따라서, Sparse data에 자주 사용된다. 곰곰이 생각해보면 BGD, SGD, Mini-batch GD, Momentum, Nesterov Accelerated Gradient 모두 모든 가중치 $\theta$에 대해 같은 learning rate를 적용시켰다. 하지만, AdaGrad는 각 가중치에 각각의 learning rate를 사용하게 된다. 즉, 다시 말해 한 모델에 $\theta$가 $i$ 개라고 가정한다면 learning rate도 $i$ 개다.
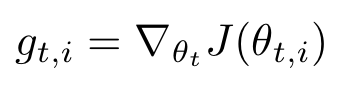
$i$개의 learning rate를 구하기 위해서 $g_{t, i}$를 사용한다. 이는 time step $t$에서 각 가중치 $\theta_{i}$의 기울기이다. 사실 이전 Optimizer도 t 인덱스를 붙이려면 붙일 수 있지만, 굳이 쓸 이유가 없기 때문에 생략한 것이다. 다음은 Gradient Descent에 t와 i 인덱스를 붙인 식이다.
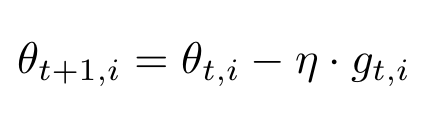
AdaGrad는 이 BGD 식에서 learning rate에 식을 추가시킴으로써 구현된다.
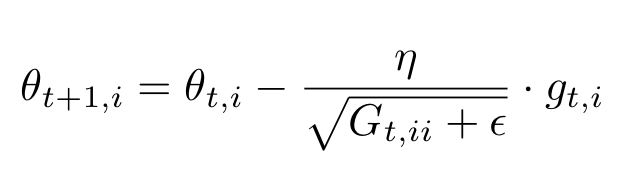
추가된 파라미터
- $G_{t, ii}$ : learning rate를 조절하는 파라미터
추가된 변수
- $\epsilon$ : 분모가 0임을 방지하기 위해 추가됨.
$G_{t, ii}$는 $i$ x $i$ 대각행렬인데 i,i 원소는 timestep t 일때까지 $g_{t,i}$의 제곱의 누적합이다.

$G_{t,ii}$는 $i$ x $i$ 대각행렬이라 하였다. 위 설명에 따라, $g_{t,i}$는 $i$차원 벡터이다.
우리는 이를 이용하여 기울기를 업데이트 해야하므로 $i$차원 벡터가 결과로 나오길 기대한다. 따라서, 아다마르곱 연산을 진행하여 $i$차원 벡터로 만든다.
AdaGrad 특징
앞에서 계속 이야기했다시피 AdaGrad는 각 가중치에 대해 각각의 learning rate를 적용함으로써 각 가중치의 상황을 고려해 최적화를 해나가는 기법이다.
AdaGrad의 장점
$G_t$는 각 가중치의 기울기의 누적합으로 이루어지므로 Sparse data를 다룰 때 강점을 보인다.
AdaGrad의 단점
$G_t$는 기울기의 제곱을 누적하기 때문에 항상 증가하게 된다. 이는 learning rate에 해당하는 부분이 0으로 수렴하게 되어 가중치 업데이트가 더이상 진행되지 않음을 의미한다. 이를 해결하기 위해 AdaDelta, RMSprop 방식이 고안되었다.
2. AdaDelta
AdaDelta는 AdaGrad의 $G_t$값이 계속 커지는 현상을 방지하기 위해서 고안되었다. 이를 위해 AdaDelta는 윈도우 방식을 이용한다. 윈도우 방식을 이용한다는 것은 현재로부터 기울기의 누적합을 윈도우 크기만큼만 고려한다는 뜻이다. 하지만, 이를 구현하기 위해선 윈도우 크기만큼의 공간을 할당해야한다. 이는 불필요한 메모리 낭비를 야기한다. 따라서, 원리는 윈도우 방식이 맞지만 지수 가중 평균(exponentially weighted average)을 이용한다.
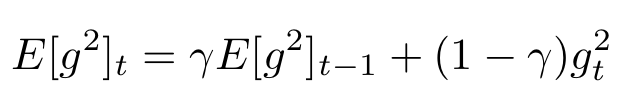
$\gamma$는 0.9를 default로 하는데 이는 Pytorch도 마찬가지다.
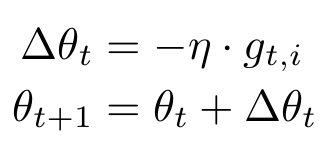
위 식은 $\Delta$(Delta)를 이용하여 BGD를 표현한 식이다.
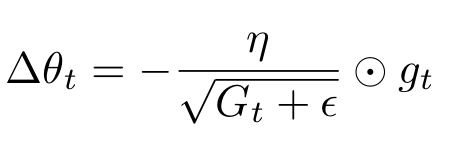
AdaGrad는 다음과 같이 표현되고, AdaDelta는 $G_t$ 부분을 $E[g^2]_t$로 표현한다. 따라서, AdaDelta 식은 다음과 같다.
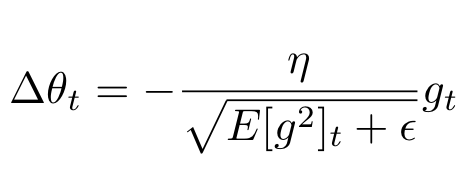
분모에 해당하는 $\sqrt{E[g^2]_t + \epsilon}$ 은 RMS(Root Mean Square)형식이므로 $RMS[g]_t$로 표현한다면 식은 다음과 같다.
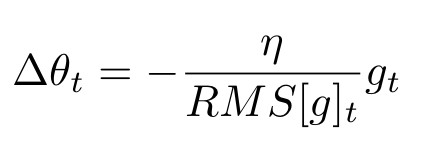
그런데, 저자는 이 $\Delta \theta$의 단위가$\theta$ unit의 역수를 따르는 점을 지적하며 이를 unit으로 수정하기 위해 다음과 같은 식 변형을 진행하였다.

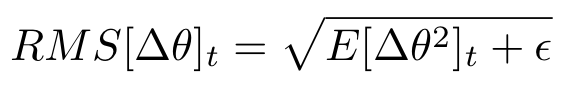

추가된 파라미터
- $\gamma$ : 윈도우 사이즈를 결정하기 위한 파라미터
AdaDelta 특징
1. 분모의 값이 단조 증가하는 AdaGrad의 단점을 보완하였다.
2. learning rate가 파라미터에서 제거되었다.
AdaDelta 장점
AdaGrad의 장점을 그대로 유지하면서 Exponentially Weighted Average를 사용하기 때문에 무작정 learning rate가 작아지는 것이 아니라 기울기의 변화량이 크면 작아지고, 기울기의 변화량이 작으면 커지는 효과를 가진다.
3. RMSprop
RMSprop은 Geoffry Hinton 교수님에 의해서 제안되었다. RMSprop은 AdaDelta와 독립적으로 개발했음에도 매우 유사하다.
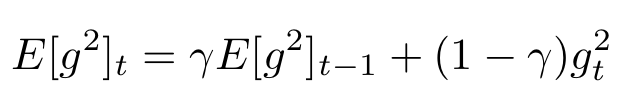
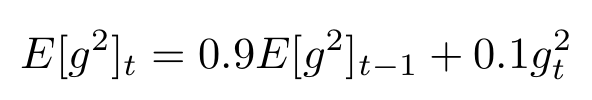
위 식은 AdaDelta의 핵심 식이고, 아래 식은 RMSprop의 핵심 식이다.

추가된 파라미터
없음.
RMSprop 특징
1. $\gamma$를 0.9로 설정하였다.
2. learning rate를 다시 하이퍼 파라미터로 되돌려놓았다.
'Deep Learning > Optimization' 카테고리의 다른 글
| Adam Optimizer (0) | 2022.09.28 |
|---|---|
| Momentum / Nesterov Accelerated Gradient (0) | 2022.09.21 |
| Gradient Descent (0) | 2022.09.18 |
| Optimizer (0) | 2022.08.09 |




