- Weight initialization
- image classification
- LeNet 구현
- Optimizer
- overfeat
- 딥러닝
- Convolution 종류
- object detection
- SPP-Net
- deep learning
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Today
- Total
I'm Lim
Gradient Descent 본문
Paper
Ruder, Sebastian. "An overview of gradient descent optimization algorithms." arXiv preprint arXiv:1609.04747 (2016).
논문이 가지는 의미
다양한 optimization 기법을 통해 어떠한 이유로 optimization이 발전해왔는지에 대해 고찰해볼 수 있다. 또한, 어떤 optimization 기법을 사용해야 될지에 관한 직관을 키울 수 있다.
1. Vanilla Gradient Descent (Batch Gradient Descent; BGD)

하이퍼 파라미터
- $\eta$ : learning rate로써 계산된 loss function의 gradient를 얼만큼 weight 업데이트시 반영할 것인가를 결정하는 파라미터
파라미터
- $\theta$ : 가중치 파라미터
BGD 특징
가중치를 한번 업데이트 시키는데 전체 데이터셋(Batch)을 이용한다.
BGD 장점
전체 데이터셋을 이용하여 업데이트 시키기 때문에 안정적이다.
BGD 단점
전체 데이터셋을 이용하여 업데이트 시키기 때문에 학습하는 데 시간이 오래걸린다. 또한, 데이터 셋의 크기가 매우 크다면 한정된 메모리에 데이터셋을 모두 올릴 수 없다.
2. Stochastic Gradient Descent (SGD)

하이퍼 파라미터
- $\eta$ : learning rate로써 계산된 loss function의 gradient를 얼만큼 weight 업데이트시 반영할 것인가를 결정하는 파라미터
파라미터
- $\theta$ : 가중치 파라미터
SGD 특징
가중치를 한번 업데이트 시키는데 데이터 셋중 하나의 샘플을 이용한다. Stochastic이란 이름의 이유는 하나의 샘플을 추출할 때 확률적(Stochastic)으로 추출하기 때문이다.
SGD 장점
가중치를 업데이트 할 때, 하나의 샘플만을 이용하기 때문에 학습 속도가 빠르다.
SGD 단점
하나의 샘플만을 이용하기 때문에 local minimum과 saddle point에 빠지기 쉽다는 단점이 있고, BGD에 비해 불안정하다.
Batch Gradient Descent vs Stochastic Gradient Descent

BGD는 SGD에 비해 안정적이다. 그러나, 학습에 걸리는 시간은 SGD가 빠르다.
3. Mini-batch Gradient Descent
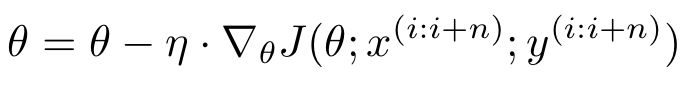
하이퍼 파라미터
- $\eta$ : learning rate로써 계산된 loss function의 gradient를 얼만큼 weight 업데이트시 반영할 것인가를 결정하는 파라미터
파라미터
- $\theta$ : 가중치 파라미터
Mini-batch GD 특징
가중치를 한번 업데이트 시키는데 데이터 셋중 미니 배치 개수만큼의 샘플을 이용한다. 위 식에서는 n개만큼의 미니배치를 이용하여 가중치를 한번 업데이트 시킨다.
Mini-batch GD 장점
1. SGD가 하나의 샘플을 이용해서 업데이트함으로써 생기는 불안정성을 줄여준다.
2. BGD가 전체 데이터셋을 이용하여 업데이트함으로써 학습하는 데 시간이 오래 걸린다는 단점을 보완한다.
Mini-batch GD 단점
1. 적절한 learning rate나 mini-batch size를 구하는 것이 어렵다. 이 파라미터는 결국 heuristic(실험적)이라고 알려져있다. 이 learning rate를 가변적으로 적용하기 위해서 AdaGrad 계열 Optimizer가 고안되었다.
2. Saddle point에 빠질 가능성이 높다. 사실, 우리가 다루는 데이터들은 보통 고차원일 때가 많고, 이러한 상황에서는 local minimum 문제보다 saddle point의 문제가 더 자주 발생하는데 이를 Mini-batch Gradient Descent는 해결하지 못한다. 이를 해결하기 위해 Momentum 계열 Optimizer가 고안되었다.
'Deep Learning > Optimization' 카테고리의 다른 글
| Adam Optimizer (0) | 2022.09.28 |
|---|---|
| AdaGrad / AdaDelta / RMSprop (0) | 2022.09.26 |
| Momentum / Nesterov Accelerated Gradient (0) | 2022.09.21 |
| Optimizer (0) | 2022.08.09 |




