- SPP-Net
- deep learning
- overfeat
- Optimizer
- LeNet 구현
- image classification
- Weight initialization
- object detection
- 딥러닝
- Convolution 종류
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Today
- Total
I'm Lim
[논문 정리] Pre activation ResNet 본문
Paper
He, Kaiming, et al. "Identity Mappings in Deep Residual Networks." arXiv preprint arXiv:1603.05027 (2016)
Abstract
본 논문에서는 Residual Block의 연산과정에 대해 분석하고, 이를 통해 새로운 Residual Block을 고안한다.
Introduction

기존 ResNet 논문에서는 Fig. 1 (a)의 residual block을 사용했다. 이를 수식으로 풀면 다음과 같다.

여기서, $h(x_l)$는 identity mapping을 의미하며, $F(x_l, W_l)$은 residual mapping을 의미한다. 또한, $f(y_l)$은 ReLU activation을 적용시킨다는 의미다.
저자의 연구에 따르면, $h(x_l)$과 $f(y_l)$이 identity mapping일 때 forward 방향과 backward 방향 모두에서 데이터가 직접적으로 전달된다고 한다. 이 조건을 만족하는 구조가 Fig. 1 (b)이다.
또한, 기존의 상식으로 여겨지던 "Activation function은 Weight 연산 이후에 적용되어야한다"는 규칙을 Fig. 1 (b)처럼 깨버림으로써 학습이 더 잘되고, 일반화도 더 잘되는 결과를 얻었다고 한다. Activation function이 weight 연산 이전에 먼저 적용이 되어서 이 모델의 이름을 "Pre-activation ResNet"으로 명명했다.
Anaylsis of Deep Residual Networks
위의 식에서 $h(x_l)$이 identity mapping이라면 $h(x_l) = x_l$이고, $f(y_l)$이 identity mapping이라면 $y_l = x_{l+1}$이 된다.
따라서, 식을 정리하면 다음과 같다.


이 재귀식에서 중요한 성질들을 관찰할 수 있다.
1 ) 아무리 L이 깊더라도, 모델은 $x_l$ 과 $\Sigma_{i=l}^{L-1} F(x_i, W_i)$ 로 구성된다. 즉, $L$ 과 $l$ 유닛들로 이루어진다.
2 ) $x_L = x_0 + \Sigma_{i=0}^{L-1} F(x_i, W_i)$이므로, $x_0$와 이전 모든 Residual function들의 합으로 볼 수 있다.
그렇다면, Back-propagation은 다음과 같이 표현된다.
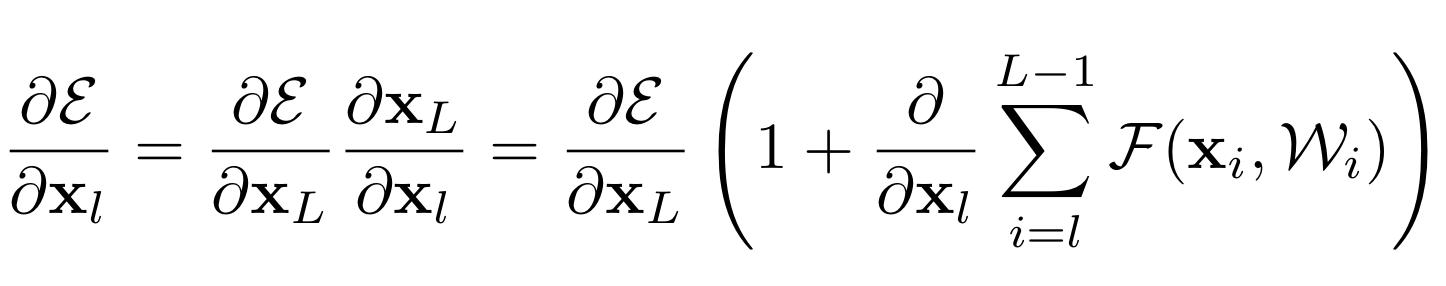
위 식을 보면, $\epsilon$에 대한 $x_l$의 편미분은 2개의 식의 합으로 나눠진다.
1 ) 전자 식 : weight layer와는 관계없이 정보를 전달한다.
2 ) 후자 식 : weight layer를 통해서 정보가 전달된다.
On the Immportance of Identity Skip connections
이 부분에서는 $h(x_l)$이 identity mapping이 아니면 어떤 결과를 낳는지에 대한 실험을 진행하였다.
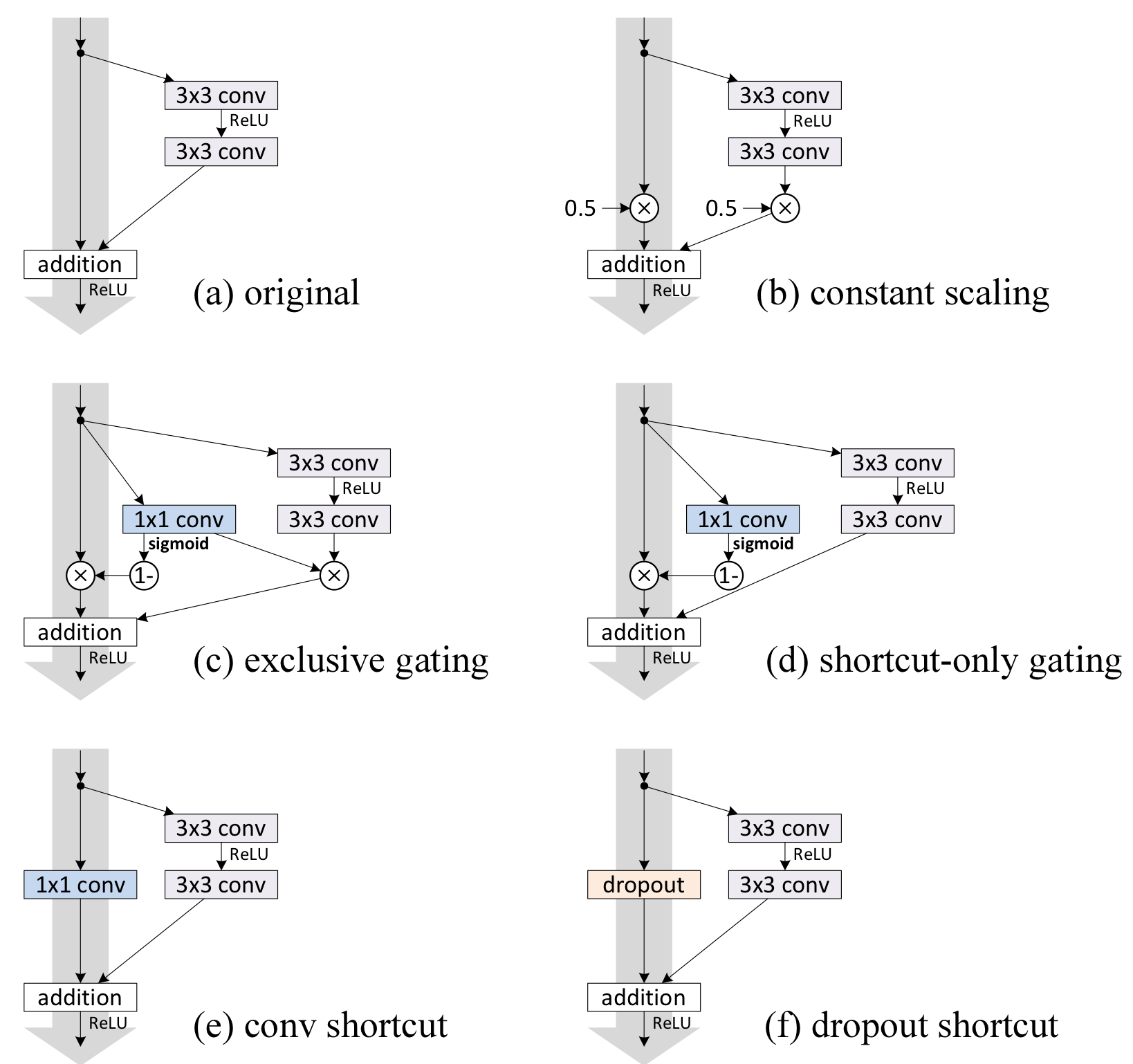
1. Scalar : $h(x_l) = \lambda_l x_l$
이렇게 스칼라 값을 하면, back-propagation시 스칼라 값이 중첩되서 곱해지게 된다. 그 결과, $\lambda_l$이 1보다 작으면 vanishing gradient problem이, 1보다 크면 exploding gradient problem이 발생하게 된다. 이는 최적화를 어렵게 만든다.
2. Exclusive gating
이는 간단히 말해서, 1 x 1 conv 연산 결과에 softmax를 적용시키고, 그 값을 이용하여 적절한 비율만큼 residual mapping과 identity mapping에 곱해주는 방식이다.
3. Shortcut-only gating
이는 Exclusive gating과 유사하지만, residual mapping 부분은 softmax 출력 값과 관계없이 그대로 더해지는 방식이다.
4. 1 x 1 Convolution
이는 identity mapping을 1 x 1 shortcut connection으로 교체한 방식이다.
5. Dropout shortcut
identity mapping에 dropout을 0.5만큼 적용시키는 방식이다. 이는 Scalar를 0.5로 둔것과 유사하게 볼 수 있다.
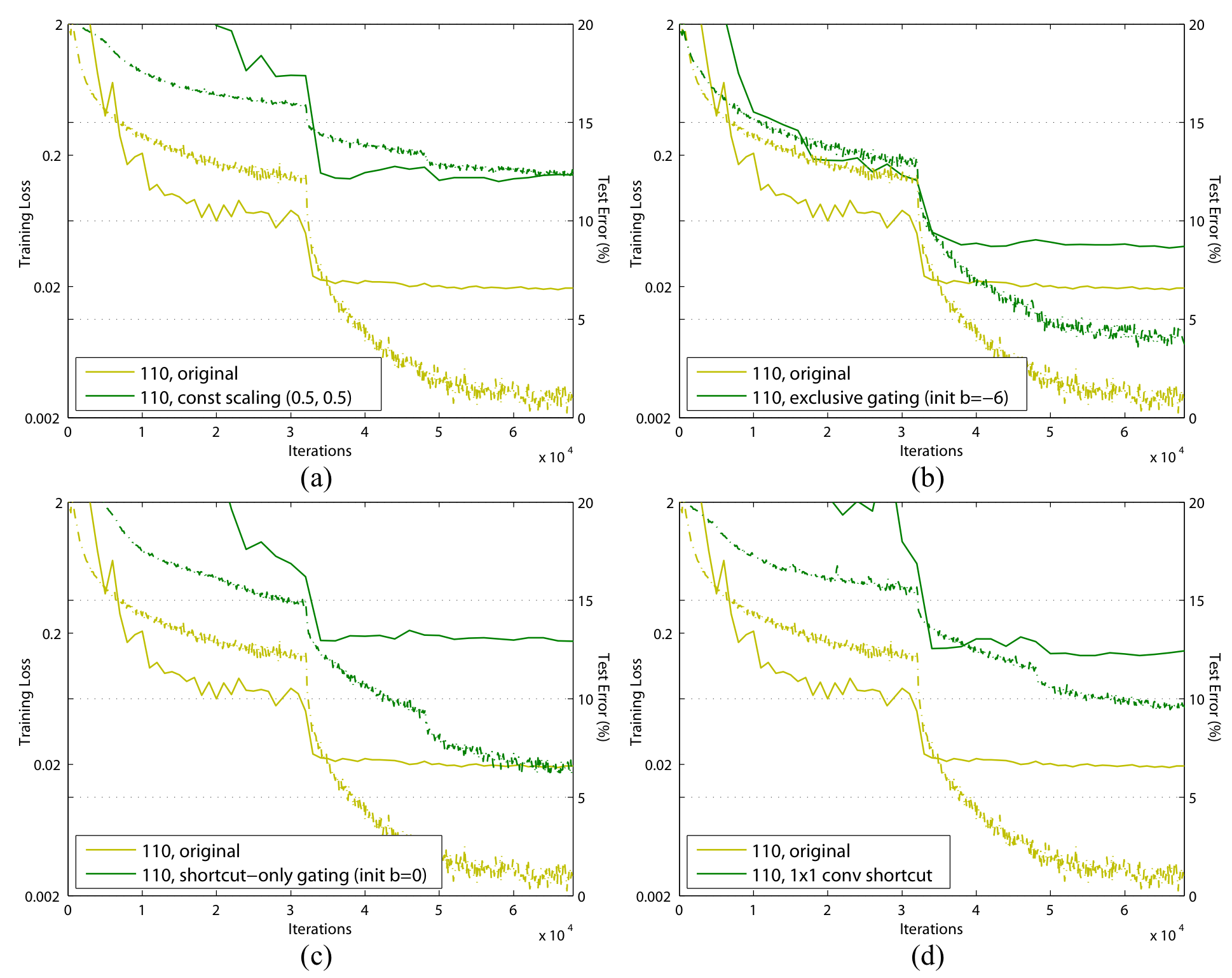
결과를 보면, 모든 경우 기존의 ResNet보다 성능이 좋지 않음을 알 수 있다.
On the Usage of Activation Functions
이 부분에서는 $f(y_l)$이 identity mapping이 아니면 어떤 결과를 낳는지에 대한 실험을 진행하였다.
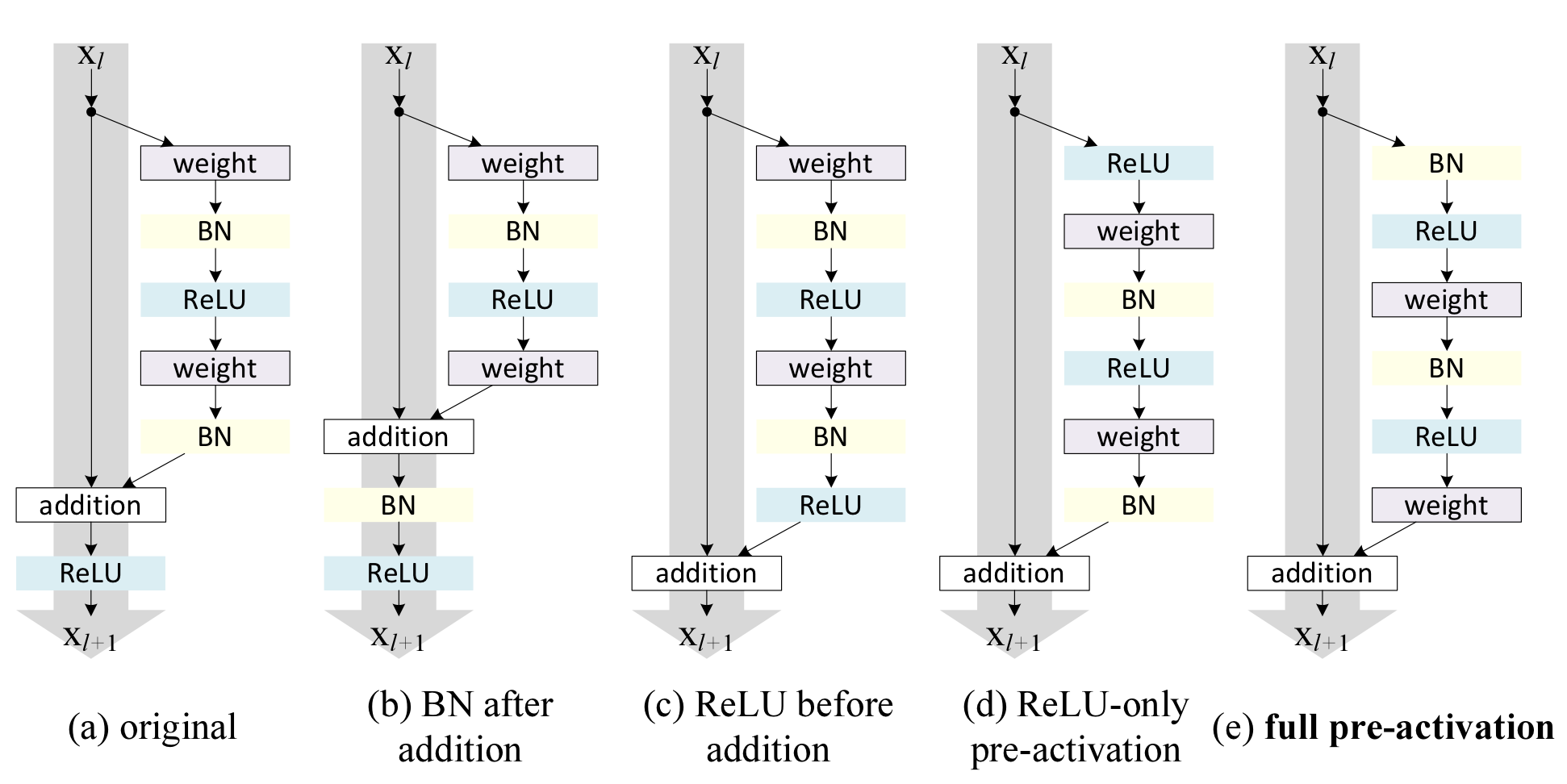
1. BN after addition // $f$ : BN + ReLU
이 방식은 element-wise addition 이후에 BN을 넣고, ReLU를 적용시킨다. 이 방식은 기존의 방식보다 성능이 안좋았다고 한다.
2. ReLU before addition // $f$ : identity mapping
이 방식은 element-wise addtion 이전에 ReLU를 적용시킴으로써, $f$를 identity mapping으로 만들었다. 그러나, residual mapping의 결과가 0에서부터 무한대까지로 제한된다. 즉, forward propagation값이 단조 증가해버리는 문제가 생긴다.
3. ReLU-only pre-activation // $f$ : identity mapping
이 방식은 2의 문제를 해결하기 위해 ReLU를 weight Layer 이전에 적용시켰다.
4. full pre-activation // $f$ : identity mapping
3의 방식을 따르면, BN의 효과를 누릴 수가 없다. 따라서, BN을 ReLU이전에 적용시킨다.

결과를 보면, 2의 방식을 적용시킨 경우는 성능이 안좋아진 반면, 4의 방식을 사용했을 때는 기존의 방식과 유사한 성능을 보였다.
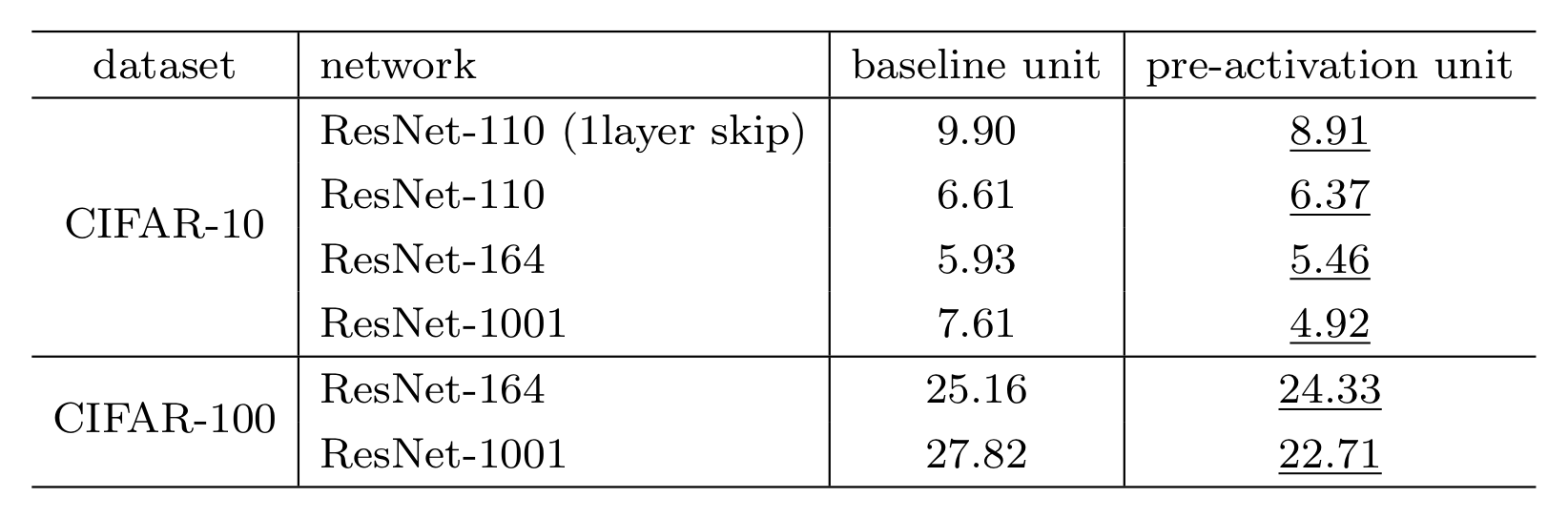
그러나, 기존의 ResNet은 layer 깊이를 1001개로 늘렸을 때 Overfitting이 발생하는 반면 pre-activation ResNet은 Overfitting이 발생하지 않았다고 한다.
그 이유로 저자는 기존의 ResNet에서는 Weight Layer의 입력이 unnormalize상태이지만 (BN이 먼저 적용되지 않았으므로), pre-activation에서는 normalize된 상태 (BN이 먼저 적용되었기 때문에)이기 때문일 것이라고 추측하였다.
Result
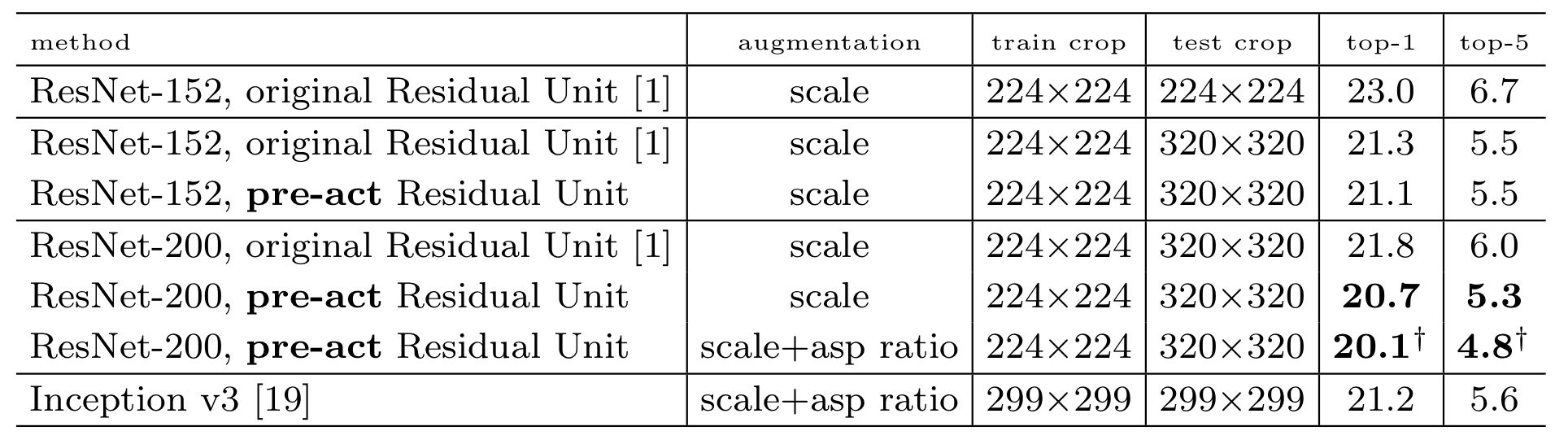
Pre-activation ResNet은 top-1 error를 20.1%, top-5 error를 4.8%로 기록하면서 기존의 ResNet의 성능을 앞섰고, Inception V3도 앞선 결과를 보여주었다.
Discussion
본 논문에서는 기존의 ResNet에서 약간 부족하게 느껴지던 수학적인 근거를 명확히 제시하고, 이를 통해 개선점을 찾아내고 개선하였다.
'Classification' 카테고리의 다른 글
| [논문 정리] DenseNet (0) | 2022.11.26 |
|---|---|
| [논문 정리] Inception v4 (0) | 2022.11.20 |
| [논문 정리] ResNet (0) | 2022.11.20 |
| [논문 정리] Inception v2, v3 (0) | 2022.11.20 |
| [논문 정리] GoogLeNet ( Inception v1 ) (1) | 2022.11.11 |




