- Optimizer
- object detection
- image classification
- overfeat
- SPP-Net
- Weight initialization
- deep learning
- 딥러닝
- LeNet 구현
- Convolution 종류
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Today
- Total
I'm Lim
Batch Normalization 본문
Paper
Ioffe, Sergey, and Christian Szegedy. "Batch normalization: Accelerating deep network training by reducing internal covariate shift." International conference on machine learning. PMLR, 2015.
Abstract
- 이전 레이어의 파라미터 값들 ( $ W, b $ )이 변하면, 현재 레이어 입력의 분포도 변한다. 이는 learning rate를 작게, weight initialization을 굉장히 예민하게 요구함으로써 학습속도를 늦춘다. 심지어, activation value가 saturation region으로 빠지게 만들 위험도 커진다. 이 현상을 Internal covariate shift라고 한다.
- 이 문제를 해결하기 위해서 mini-batch별로 데이터를 normalization시키는 것이 Batch Normalization이다.
- Batch Normalization은 weight initialization의 영향을 줄이고, learning rate도 높게 설정할 수 있게 해준다. 또한, Regularizer로써의 역할도 수행하여 특정 경우에 한해 Dropout을 안써도 된다고 한다.
Introduction
- 입력 분포가 training과 test 데이터에 대해 같은 분포를 가진다면 훨씬 더 빠르게 학습을 하게 될 것이다.
딥러닝 모델은 back-propagation 연산을 통해 Weight를 업데이트 함으로써 학습을 진행한다. 이 weight가 업데이트 되는 동안 layer의 입력 분포는 계속 변화한다. $(Y = \sigma (\Sigma WX))$ 이는 레이어들이 계속해서 새로운 분포를 학습하게 만든다. 만약, 입력 분포가 training과 test 데이터에 대해 같은 분포를 가진다면 훨씬 더 빠르게 학습을 하게 될 것이다.
- 입력 분포가 고정되어있는 것은 activation value가 saturation region으로 빠지지 않게 도와준다.
입력 분포가 고정되어있는 것은 activation value가 saturation region으로 빠지지 않게 도와준다. 예를 들어, activation function이 sigmoid라고 가정하자. 그리고, sigmoid의 입력인 $x$의 절댓값이 증가한다고 가정하자. 이는, 많은 activation value가 saturation region으로 빠지게 만든다. 물론, 이러한 현상 ( gradient vanishing )은 ReLU가 나오면서 해결되었지만 그럼에도 불구하고, activation function의 입력분포가 안정적이라면 optimizer가 saturation region에 덜 빠지게 될것이고, 학습을 더욱 빠르게 할 것이다.
Internal covariate shift
internal covariate shift란 학습도중 weight값의 변화에 따라 각 레이어 입력 분포가 달라지는 현상을 말한다.
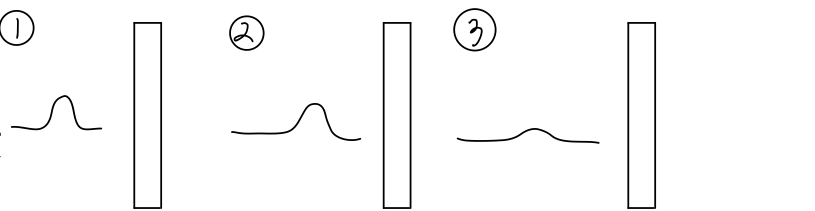
한 레이어의 연산이 $Y = \sigma (\Sigma WX)$로 이루어지는 걸 생각하면 당연한 이야기다.
Reducing Internal Covariate Shift
이 internal covariate shift의 해결방안은 무엇이 있을까?
- 데이터를 직접 수정
$i$ 레이어의 입력이 $u_i$라고 하자. $i$ 레이어의 이전 레이어를 $j$라고 한다면 $u_i = WX_j + B_i$가 된다. 그러면, $X_i = WX_j + B_i$가 되고, $E[X_i] = WE[X_j] + B_i$가 된다. $X_i$에서 평균을 빼주는 scaling을 진행한다고 가정하였을때, $X_i - E[X_i] = WX_j + B_i - (WE[X_j] + B_i) = WX_j - WE[X_j]$가 된다. 즉, bias가 연산에서 제외된다. 그래서 b의 변화와 차후의 scaling의 조합이 layer의 출력을 변화시키지 않게된다. 즉, loss에 영향을 끼치지 않게되고, 그 결과 bias가 무한히 증가한다. 이 문제는 normalization을 진행하여도 동일하게 발생하고, 논문에서는 실험적으로 확인하였다고 한다.
- Optimizer 수정
위에서처럼 데이터를 직접 수정시키게 되면 optimizer가 scaling을 무시해버리게된다. 이것을 해결하기 위해서, 옵티마이저를 수정하는 방식을 사용할 수 있을 것이다. 이를 위해, $\dfrac {\partial Norm(x, X)}{\partial x}$와 $\dfrac {\partial Norm(x,X)}{\partial X}$를 구해야하는데 연산량이 커서 사용하기에 부적합하다고 한다.
- Batch Normalization
이를 해결하기 위해 논문에서는 Batch Normalization을 적용하였다.

LeNet 논문에서 whitening이 아닌 normalization만으로도 학습속도가 개선이 되었음을 보여서 이 논문에서도 normalization을 적용시킨다.

또한, 학습가능한 파라미터로 $\gamma$와 $\beta$를 사용한다. 그 이유는 만약 sigmoid function에 들어갈 입력에 normalization만을 적용시키면 출력값이 입력값과 일대일 대응이 되어버린다. 이는 activation function의 역할인 nonlinearity를 없애버리게 되어 옳지 못하다. 따라서, $\gamma$ 와 $\beta$를 사용함으로써 최적의 경우에 Batch Normalization이 없는 것처럼 행동할 수 있도록 만들겠다는 의도로 보인다. 그 근거로, 논문에서는 $\gamma^{(k)}$값을 $\sqrt {Var[x^{(k)}]}$로 두고, $\beta^{(k)}$값을 $E[x^{(k)}]$값으로 두면 원래의 $x^{(k)}$를 복원할 수 있다고 설명한다.
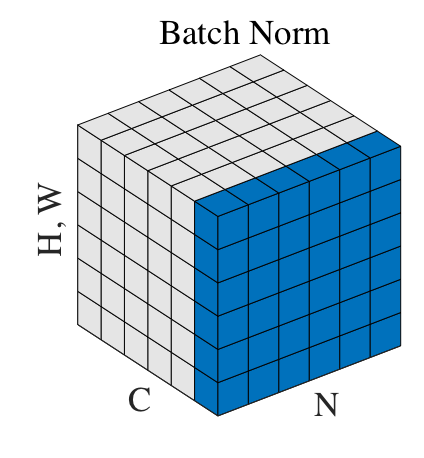
일반적으로 학습시킬 때, mini batch를 사용하여 학습시키므로 논문에서는 각각의 미니 배치의 평균과 분산을 표본으로 보았다. 이를 이용하여 모델 평가시에 고정된 평균과 분산을 적용시킨다.

위 그림은 학습시에 어떻게 평균과 분산을 구할 것인지에 관한 알고리즘이다.

위 그림은 학습 및 평가시에 어떻게 평균과 분산을 적용할지에 관한 알고리즘이다.
학습시에는 미니배치별로 평균과 분산을 구하고, $\gamma$와 $\beta$는 Optimizer에 의해서 학습된다. ( 1 - 7 )
평가시에는 이미 학습된 $\gamma$와 $\beta$를 사용한다. 주의할 점은 평가시 $E[x]$와 $Var[x]$를 학습시에 사용하였던 미니 배치의 평균과 분산을 이용하여 구한다는 점이다. ( 8 - 12 )
따라서, Batch normalization은 미니 배치를 normalization 시킴으로써 동작하는 알고리즘이라 할 수 있다.
Conclusion
Batch Normalization을 적용시켰을 때, 학습속도가 훨씬 개선되었고 성능 또한 좋아졌다고 한다.
개인적인 생각
딥러닝 모델에서 데이터라 함은 입력 데이터와 출력데이터, 그리고 모델 내부 각 레이어의 입력 데이터가 있다고 생각한다. Batch Normalization은 이 모델 내부의 데이터를 normalization 시킴으로써 weight값이 exploding하거나 vanishing 하는 문제를 줄여 학습속도를 개선시키지 않았을까 생각한다.
